Olympic Gymnastics Prediction


Using statistical methods to get medal probabilities



Aidan Bramer

Department of Mathematics
University of Dayton

Background

This study will look at possible female Olympic gymnasts

  • Goal: to predict medal probabilities for each athlete in there event

  • Find the athletes who will participate in each event

  • test different ways to predict athletes scores

  • simulate athletes scores

  • observe each athletes probability

Data Structure

LastName FirstName Gender Country Date Competition Round Location Apparatus Rank D_Score E_Score Penalty Score
6772 Makovits Mirtill w HUN 11-14 Aug 2022 2022 Senior European Championships qual Munich, Germany BB 65 4.5 6.900 NA 11.400
3665 Gobadze Ani w GEO 11-16 Apr 2023 2023 10th Senior European Championships qual Antalya, Turkey UB 110 3.2 6.266 NA 9.466
5403 Kinsella Alice w ENG 29 Jul-2 Aug, 2023 BIRMINGHAM 2022 Commonwealth Games final Birmingham, England FX 1 5.6 7.766 NA 13.366
8796 Petrova Marija w LAT 11-16 Apr 2023 2023 10th Senior European Championships qual Antalya, Turkey VT1 100 3.4 8.500 NA 11.900

General structure is 5008 rows 16 columns.

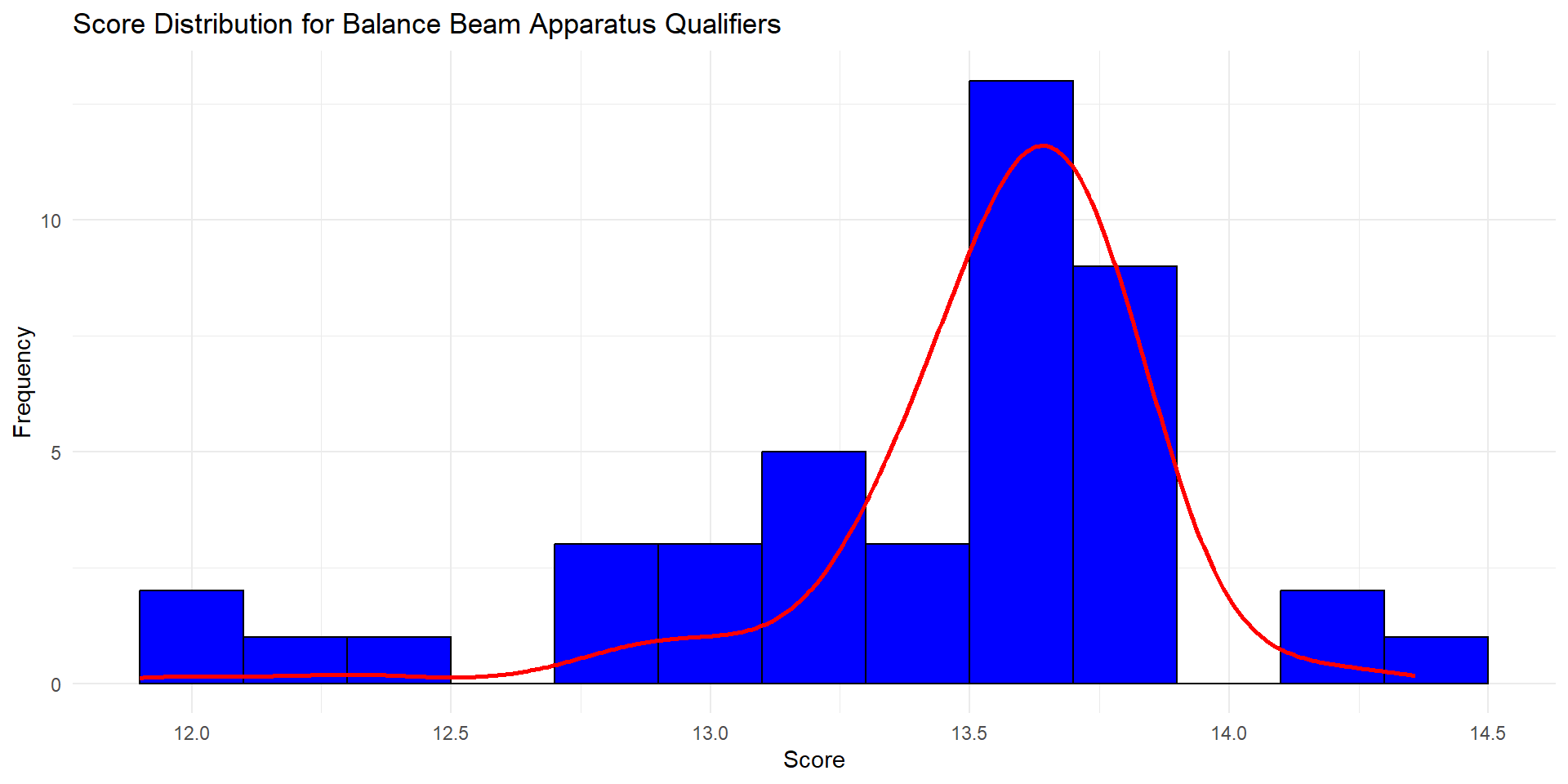
Balance Beam

For time constraints and due to repetition we are going to look at one event.

  • Find the top 8 athlete who qualified for the Olympics
  • Predict Possible Scores for these Athletes
First Name Last Name Score
396 Andrade Rebeca 12.733
1189 Black Elsabeth 13.566
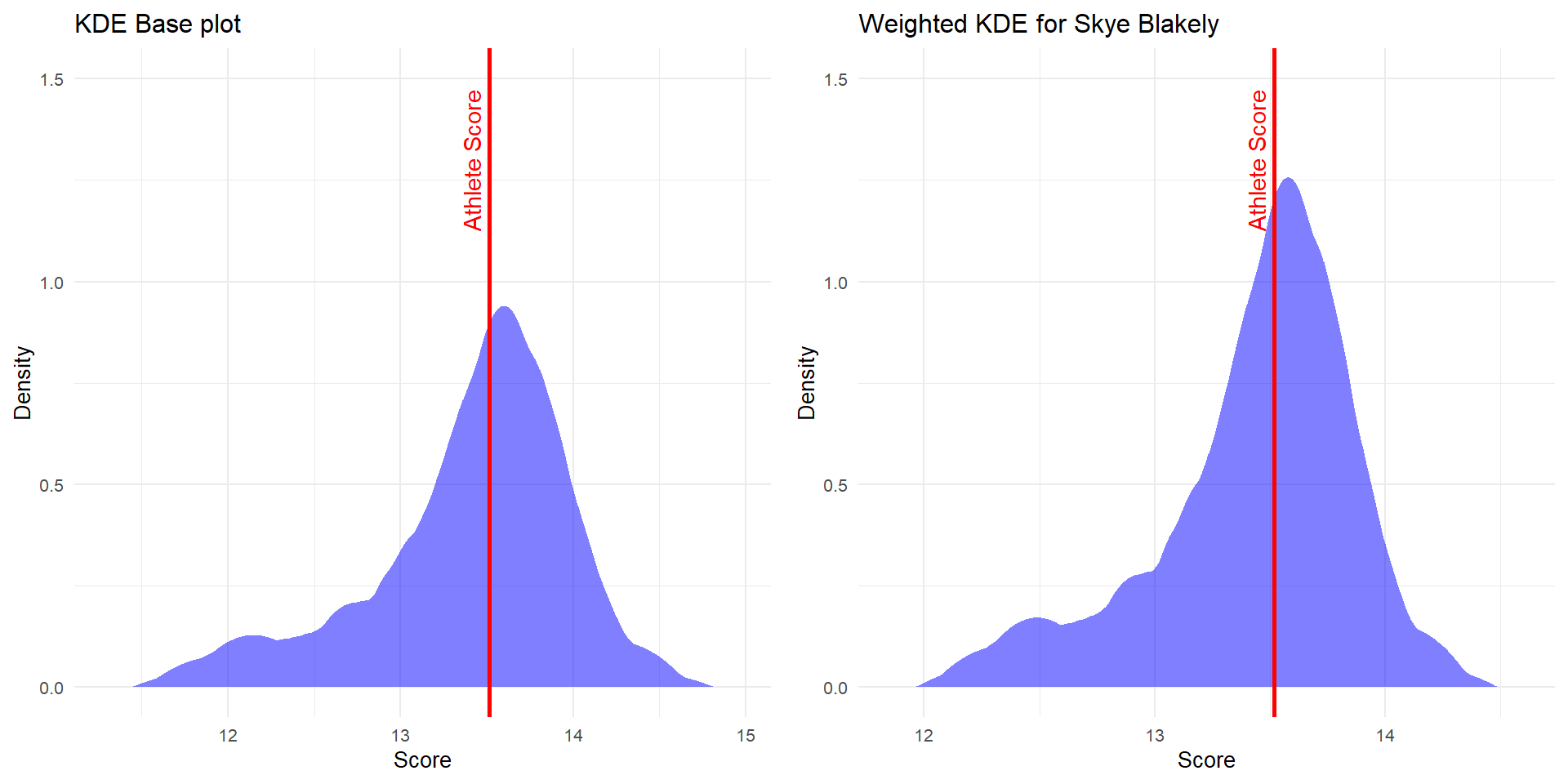
1201 Blakely Skye 13.300
1265 Boyer Marine 13.300
5692 Kovacs Zsofia 12.733
7487 Miyata Shoko 13.533
8445 Ou Yushan 13.000
12036 Watanabe Hazuki 13.600

History for these 8 Athletes

Looking at the history of all the athletes scores we can see the number of data points available.

To qualify for the Olympics every athlete will have at least 2 scores based on the two Olympic qualifying rounds.

First Name Last Name Data Points Count
Elsabeth Black 4
Hazuki Watanabe 3
Marine Boyer 9
Rebeca Andrade 4
Shoko Miyata 7
Skye Blakely 2
Yushan Ou 7
Zsofia Kovacs 7

Model Building

  • Based on each athlete having a different number of scores it caused a problem in a regression approach
  • First there would be a need to use summary statistics for each athlete
  • This approach caused a problem because if an athlete had less data points then they only had the Olympic qualifying scores-biased
  • Hard to justify using all athletes scores to predict only the best athletes
  • the assumption: if these are 8 best athletes then they would have a similar athletic performance

Basics of Kernel Density Estimator

For KDE, the formula is:

\[ f_h(x) = \frac{1}{nh} \sum_{i=1}^n K\left(\frac{x - x_i}{h}\right) \]

Where:

\(x_i\) are the data points.

\(K\) is the kernel (e.g., Gaussian).

\(h\) is the bandwidth, controlling the smoothness.

Weighted KDE

Weighted KDE allows different weights for different data points.

The formula is:

\[ f_h(x) = \frac{1}{nh} \sum_{i=1}^n w_i K\left(\frac{x - x_i}{h}\right) \]

Where \(w_i\) are the weights for each data points

  • Have to select weights, kernel and bandwidth

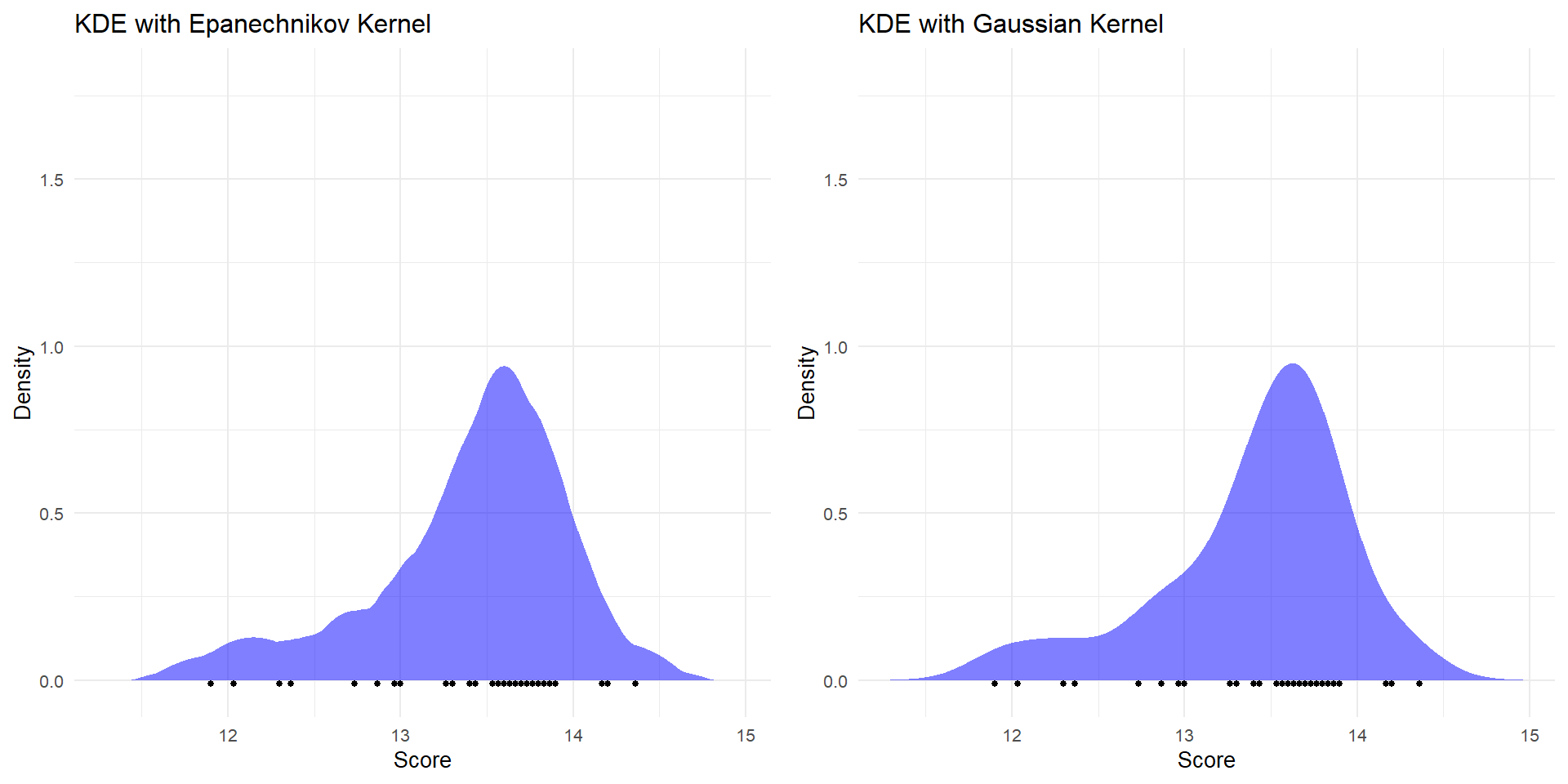
Weighted Kernel Density Estimator Approach

Gaussian Kernel: The Default

The Gaussian (or Normal) kernel has the form:

\[ K(u) = \frac{1}{\sqrt{2\pi}} e^{-\frac{1}{2} u^2} \] ( u ) represents the standardized distance: \[ u = \frac{x - x_i}{h} \] Characteristics: Infinitely long tails Smooth, bell-shaped curve. Influences the KDE even at considerable distances

Epanechnikov Kernel: An Alternative

The Epanechnikov kernel has the form:

\[ K(u) = \frac{3}{4}(1 - u^2) \quad \text{for } |u| \leq 1 \]

Characteristics:

  • Compact support (zero outside the range [-1, 1])
  • Parabolic shape
  • Considered “optimal” in a mean integrated squared error sense

Why Epanechnikov?

  1. Compact Support: The Epanechnikov kernel ensures only nearby points contribute to the density, which is beneficial for small datasets. Distant points don’t influence the KDE.

  2. Locality with Weights: Weights can be effectively accounted for within the local neighborhood of each data point without being overshadowed by distant points.

  3. Less Smoothing: The Gaussian kernel might overly smooth small datasets, potentially hiding important data features. Epanechnikov captures local structures better.

Visual Comparison

Visualizing Sample Athletes Weighted KDE

Simulation Study

Elsabeth Black Hazuki Watanabe Marine Boyer Rebeca Andrade Shoko Miyata Skye Blakely Yushan Ou Zsofia Kovacs
13.78529 13.29861 13.51149 13.11144 13.82491 13.36353 13.28248 13.59079
13.41941 13.54073 13.65676 13.05226 13.37813 14.12054 12.20335 13.42937
13.82295 13.44389 12.72593 12.69181 13.64189 13.42259 13.49186 13.73606
13.48398 13.31476 13.78052 13.83771 13.85183 13.55681 13.67440 13.43475
12.53700 13.44389 13.97960 13.67093 13.90566 13.99168 12.45568 13.24105
13.51088 13.74519 13.66214 12.35288 13.52885 13.34205 13.48649 12.89670
13.34946 13.58378 12.44076 12.82093 12.15081 13.60513 13.15363 13.11730
13.77991 13.48693 12.22016 13.68169 13.49117 13.50849 13.23416 13.62845
13.02663 13.92275 13.47383 12.89624 12.78600 13.68029 13.00867 12.93974
13.34408 13.14258 13.95269 13.21903 13.70110 13.44943 13.77104 13.57464

Medal Counts

Gold Silver Bronze
Elsabeth Black 0.120 0.122 0.134
Hazuki Watanabe 0.155 0.156 0.136
Marine Boyer 0.137 0.135 0.121
Rebeca Andrade 0.060 0.081 0.100
Shoko Miyata 0.167 0.118 0.152
Skye Blakely 0.142 0.146 0.110
Yushan Ou 0.131 0.132 0.135
Zsofia Kovacs 0.088 0.110 0.112

Other Apparatus Results

Uneven Bars

Gold Silver Bronze
Elisabeth Seitz 0.123 0.126 0.149
Naomi Visser 0.050 0.094 0.104
Nina Derwael 0.166 0.171 0.132
Rebeca Andrade 0.051 0.074 0.089
Rui Luo 0.114 0.130 0.131
Sanna Veerman 0.105 0.110 0.128
Shilese Jones 0.183 0.127 0.126
Xiaoyuan Wei 0.208 0.168 0.141

Floor Routine

Gold Silver Bronze
Jade Carey 0.154 0.133 0.143
Jennifer Gadirova 0.061 0.099 0.102
Jessica Gadirova 0.216 0.161 0.131
Jordan Chiles 0.151 0.160 0.114
Martina Maggio 0.090 0.112 0.115
Naomi Visser 0.106 0.117 0.133
Rebeca Andrade 0.158 0.140 0.147
Shoko Miyata 0.064 0.078 0.115

Challenges and Limitations

  • Lack of Data for Certain Athletes
  • The goal was to get some way of sampling future events for different medals
  • The proportions generated by my assumption that these 8 athletes would have a similar history

Sources

Chu, Chi-Yang, Daniel J. Henderson, and Christopher F. Parmeter. “On discrete Epanechnikov kernel functions.” Computational statistics & data analysis 116 (2017): 79-105.

Soh, Youngsung, et al. “Performance evaluation of various functions for kernel density estimation.” Open J Appl Sci 3.1 (2013): 58-64.

NBC Olympics

Thank you

Special Thank you to my advisor Dr. Tessa Chen.

Questions?

Aidam Bramer Linkedin Profile